このフレームのURLは https://www2.kpu.ac.jp/for_ecol/Erman/Ermanii_ilts.html です
最近の研究トピック(2)-その1 研究室HPへ 隅田HPへ
関連論文 :以下の記事は次の論文の前半部分です。後半の説明は「研究トピック(2)-その2」を見てください。:
Sumida, A., Nakai, T., Yamada, M., Ono, K., Uemura, S., Hara, T. (2009) Ground-based estimation of leaf area index and vertical distribution of leaf area density in a Betula ermanii forest. Silva Fennica 43(5), 799-816. Linked to FREE journal page !
(文責=クレーム先: 隅田明洋(HPへのリンク))
樹木の葉量は地上からローテクで推定しろ!
木登りせずにパイプモデルアロメトリーで個体葉量を推定する方法
== 樹木の葉量推定:なぜ、どうやって? ==
森林樹木の葉量(葉の総面積や総重量)を知ることは、樹木の生育や森林の状態を評価するのに役立つだけでなく、森林によるCO2吸収量や、森林~大気間の水や熱の交換などを評価するうえでも非常に重要です。このため、航空機や人工衛星を使った観測などさまざまなハイテク技術が森林の葉量推定に利用されています。しかし、このハイテク技術による葉量推定を支えているのは、超ローテクな森林調査です。ハイテク技術の精度を確認するために、森林で樹木を切り倒して樹木の葉量を実際に測り、ハイテク技術による推定値と比較するのです。
とは言え、森林全部の樹木を切り倒すわけにはいきません。そこで、森林の中の何本かの木をサンプルとして選んで切り倒し、葉量を実際に測定します。しかし、いくつかの理由から、単純にそれらの平均をとるわけにはいきません。そこで使われるのが「アロメトリー(allometry)」と呼ばれる生物の形作りの規則です。
アロメトリーを簡単に言えば、個体の中のある部分の大きさや量と別の部分の大きさや量との関係を式で表したものです。例えば、人間の頭の周囲長と脳みその量との関係もアロメトリーです。一度頭の周囲長と脳みその量とのアロメトリー関係がわかれば、頭の周囲長の実測値から脳みその量を生きたまま推定することができます。樹木の葉量推定もこれと同じようにやるのです。
== 樹形のパイプモデル ==
樹木の葉量推定で最も汎用性が高いと言われているのは「樹形のパイプモデル」という考えを利用したアロメトリーです(補足1参照)。このアロメトリーの関係式について説明します。
パイプモデルのアロメトリーとは、生枝下高(なまえだしたこう;個体の中で一番低い生きた枝の直下の地上高)の幹の太さと個体の葉量との関係を表したものです(補足1)。上の例でもわかるように、パイプモデルのアロメトリーは異なる森林でも同じ樹種なら同じ式を適用できると言われています。ということは、ある森林で調べたパイプモデルアロメトリーは他の森林でも使えるので、わざわざ新たな森林で新たに木を切ってアロメトリーを作る必要はないということです。これに対して、パイプモデル以外のアロメトリー(例えば胸高直径と葉量との間のアロメトリー)は森林によってかなり変わります。それに比べると、パイプモデルアロメトリーははるかに優れています。
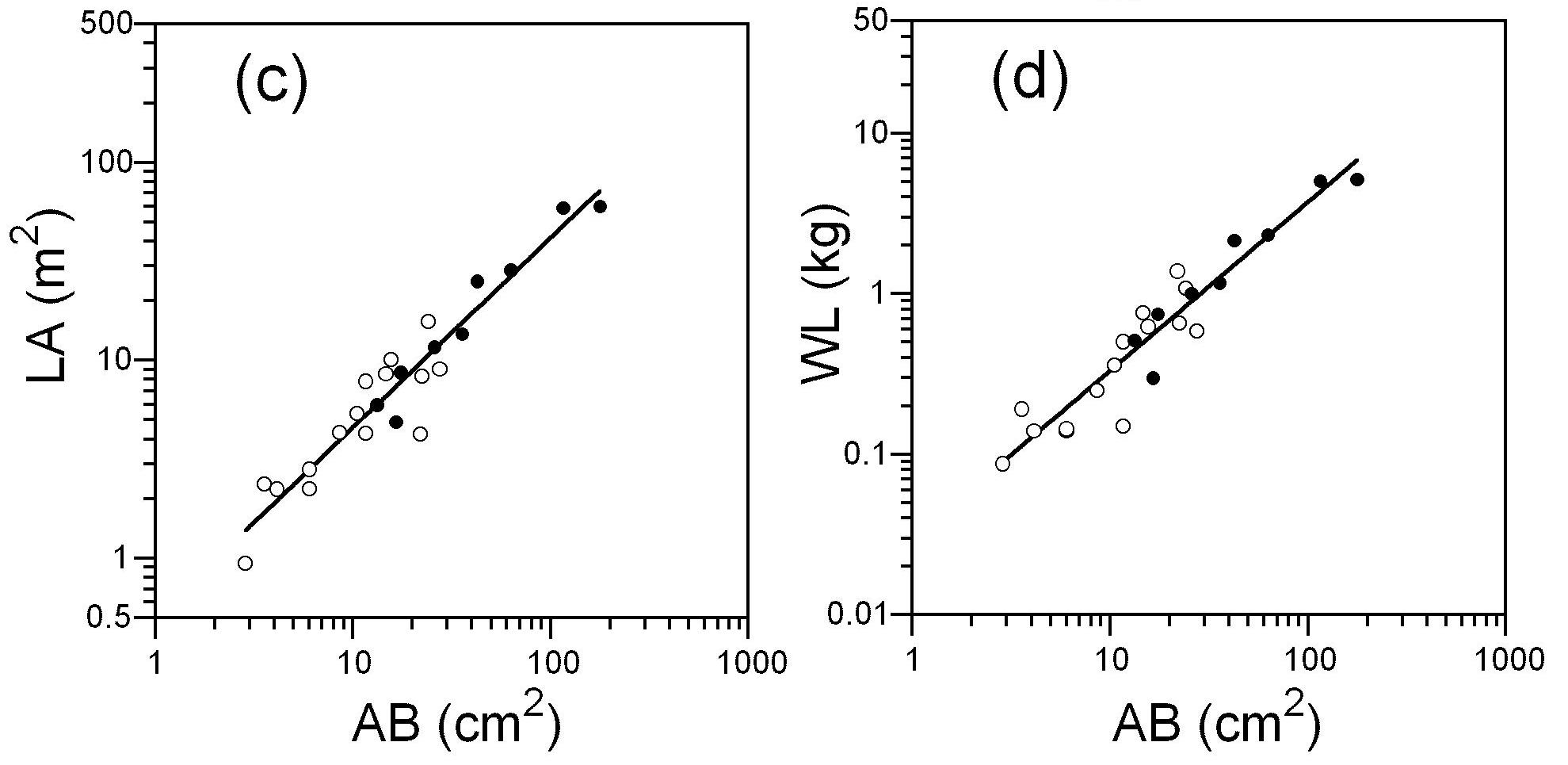
- パイプモデルのアロメトリー (落葉広葉樹 ダケカンバの例)
個体の枝下の幹断面積(横軸 "AB")と、個体の葉面積(c、縦軸 "LA")および個体の葉の乾燥重量(d、縦軸 "WL")との間のアロメトリー関係が直線で表されている(Sumida et al. (2009)のFig.2より引用)。1点1点が各々の樹木のデータ。樹齢の違う二つの森林のデータ(●と○)も1つのアロメトリー式に統一できた。
上の図のようなアロメトリーの関係式がいったん得られ、他の樹木でも同じ関係式が適用できると仮定すると、木を切らなくても個体の葉量を計算で求めることができます。木登りして、生枝下高の幹直径を測定し、その値から葉量を計算すればよいのです。さらに、森林内の樹木一本一本の生枝下高幹直径を測定し、各個体の葉量を計算して全部足すと、森林全体の葉量が推定できます。
でも、もうおわかりでしょう。パイプモデルアロメトリーには実用上大きな欠点がありました。生枝下高の幹の太さを測るためにえっさほいさっさと「木登り」しなければならないということです。
ところが最近、私たちは、木登りしなくても生枝下高の幹の太さを地上からの測定で調べる方法を発見しました。
== これで木登りせずに樹木の葉量が推定できる ==
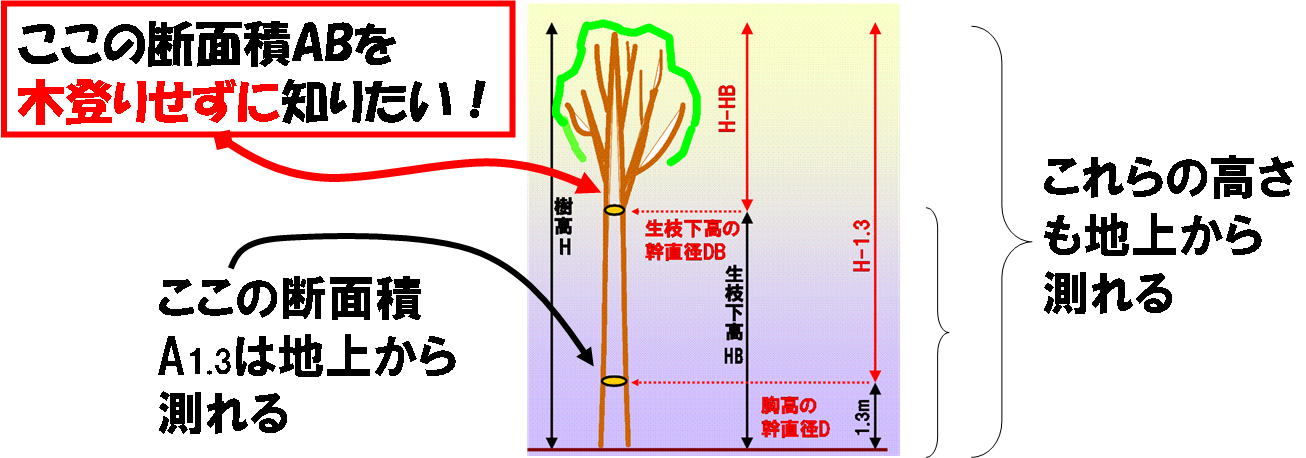
私たちがみつけたのは、上の図で、AB/(H-HB)=A1.3/(H-1.3) という単純な関係が成立しているということです。ここで、H-HBは樹冠長(樹木の最上部の高さ(H)から生枝下高(HB)までの幹の長さ)、(H-1.3)は樹木の最上部から胸高(地上高1.3m)までの幹の長さ、A1.3は胸高の幹の断面積、ABは生枝下高の幹断面積です。下の図では,上の式の意味をもっと簡単な図で説明してあります。つまり、下の図左のAの断面積とA’の長さ,Bの断面積とB'の長さとの間の関係が,A/A'=B/B'だったということなのです(下のまん中の図).この図では3つのダケカンバ林の156個体のデータがほぼ1:1の関係(点線)にのっているのがわかります(実線は回帰直線)。もしも幹全体のみかけの形が二次曲線(放物体;下の右図)ならばこの関係はいつでも成立するはずです。しかし、実際の幹の形がそうなっていないことはよく知られています。不思議ですね。
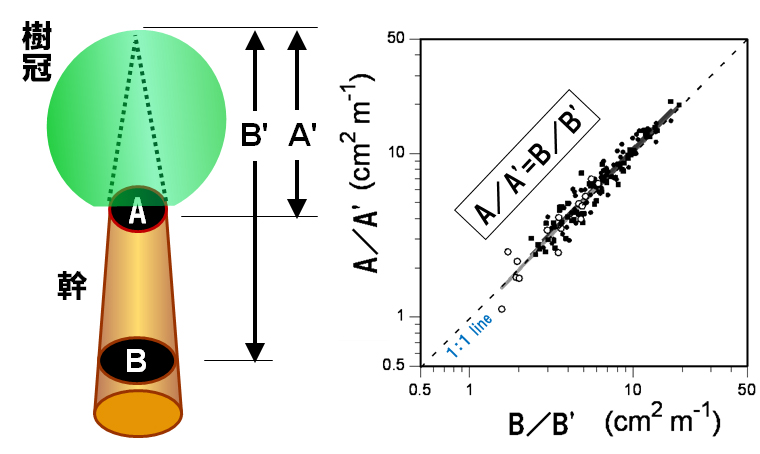

ともかく、 A/A'=B/B'ならば,AはA=A'×B/B’で求められるはずです.もとの数式で表すなら,生枝下高幹断面積ABは
AB = A1.3×(H-HB)/(H-1.3) で計算できるはずです。
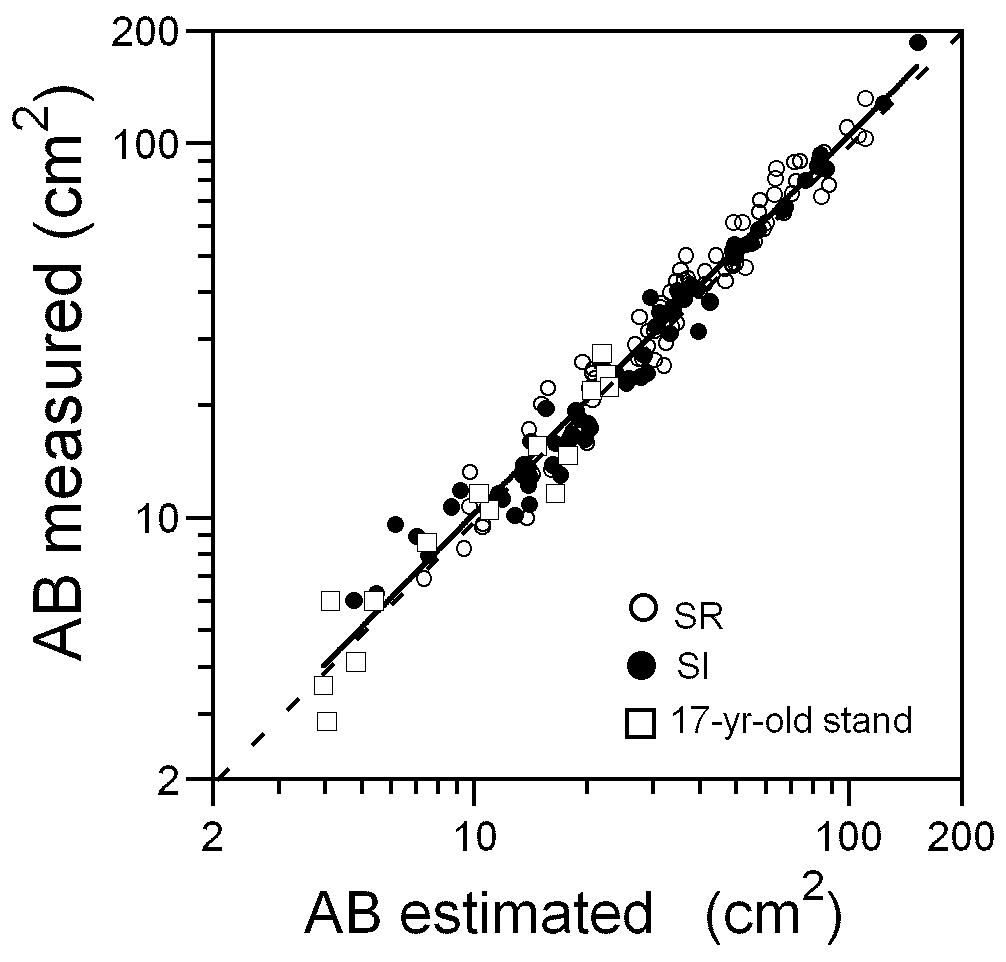
実際に木登りして測定したAB(上の図の縦軸)と、上の式の右辺で推定したAB(上の図の横軸)とを比較してみました(上の図はSumida et al. (2009)のFig.3より引用)。1:1を示す点線と実線で示した回帰直線はほとんど重なっています。つまり、正比例なのです。正比例なので、胸高の幹断面積と樹高と生枝下高の測定値があれば、どんな森林でも生枝下高幹断面積に換算できます。
胸高の幹断面積は、メジャーで測るのが一番正確です。幹の周囲長を測り、幹断面が円だと仮定して周囲長を断面積に換算します。このように、森林調査がいまだにローテクとはいえ、測定機器は進化してきました。最近では地上から樹高や生枝下高を測定できるポータブルな調査機器が市販されています。かくして、木登りしなくても生枝下高幹断面積が推定でき、したがって高所恐怖症や体力の衰えたおじさん・おばさんにもパイプモデルアロメトリーが実用上使えることになったというわけです。ああうれしい。
== これからの課題 ==
現在、過去に蓄積された熱帯から亜寒帯までのさまざまなタイプの森林のデータを解析し、ダケカンバで成立した上の関係が成り立つかどうかについて解析しています。どうもうまくいきそうです。これについてはそのうち論文発表報告します。
もうひとつ大事なこと、それは、そもそもなぜ上のような関係が成立するかという生物学的な理由がまだ明らかになっていないことです。理由がわからなければ、上の発見は偶然ダケカンバの森林で成立しただけだ、といわれても反論できません。これに答えるのは簡単ではないのですが、すでに別のデータを使った解析でその理由もわかってきました。これはまだヒミツです。お楽しみに。
おしまい
back to the page top
<<< 補足1 >>>
「樹形のパイプモデル」とは?
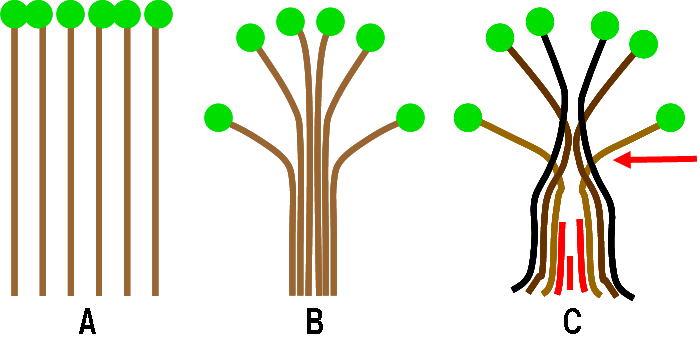
樹木が光合成をするためには、水を根から葉まで輸送するパイプが必要です。単位量の葉が光合成するためには単位量の葉に対して一定の太さのパイプを確保しなければなりません(A)。そのパイプを束ねたもの(B)が幹であると考える(単純パイプモデル)と、幹の断面積とその個体の葉の全量とは正比例するはずです。
しかし、樹木が成長を続ける間、樹木の下側の枝は十分な光を受けられず死んでしまいます。枝は落ちてしまいますが、水輸送に使われなくなった幹内部のパイプはそこにそのまま残ります(Cの赤いパイプ)。幹の下側ほど太くなっているのはこのためです。このような場合でも、生きた枝の直下(生枝下高「なまえだしたこう」と読む)の幹の断面積(Cの矢印の部分)は個体の葉量に比例しているはずです。樹木の幹の形はこのようなデザインになっているはずだ、というのが「樹形のパイプモデル」です。
樹木の幹が樹形のパイプモデルを基本として形作られているのなら、個体の樹高や地際の幹の太さが樹木間で違っていても、生枝下高の幹断面積と個体の葉量とは正比例の関係にあるはずです。
そこで、
というわけです。
- サイズの違う樹木数本を切り倒し、この幹断面積~個体葉量の間の比例関係(パイプモデルアロメトリー)をあらかじめ定式化しておき、次に、
- 残りの個々の樹木に木登りして、生きた枝直下(図Cの赤矢印)の幹断面積を調べれば、
- 生きたままそれらの葉量を計算できる、
オリジナルのパイプモデルの論文は、篠崎吉郎博士らが1964年に発表した下の二つの論文です。現在でも世界中の研究者から引用されています。
- Shinozaki et al. (1964a)A quantitative analysis of plant form - the pipe model theory I. Basic analysis. Japanese Journal of Ecology 14(3), 97-105. Link to CiNii Fulltext pdf page (FREE)(open in new window)
- Shinozaki et al. (1964b)A quantitative analysis of plant form - the pipe model theory II. Further evidence of the theory and its application in forest ecology. Japanese Journal of Ecology 14(4), 133-139. Link to CiNii Fulltext pdf page (FREE)(open in new window)
<<< 補足1 おわり:もとにもどる>>>