このフレームのURLは https://www2.kpu.ac.jp/for_ecol/Erman/MacArthurHorn_ilts.html です
最近の研究トピックから(2)-その2 研究室HPへ 隅田HPへ
関連論文 :以下の記事は次の論文の後半部分です。前半部分は「研究トピック(2)-その1」を見てください。.:
Sumida, A., Nakai, T., Yamada, M., Ono, K., Uemura, S., Hara, T. (2009) Ground-based estimation of leaf area index and vertical distribution of leaf area density in a Betula ermanii forest. Silva Fennica 43(5), 799-816.
Link to FREE journal page ; !
(文責=クレーム先: 隅田明洋(HPへのリンク))
森林の葉量の垂直分布を
携帯型レーザー距離計でしらべよう!
~ 木を切らずに広葉樹林の葉量の垂直分布を推定する方法 ~
MacArthur-Horn法の秘密についての補足はここ→(PDF)
「研究トピック(2)のその1 樹木の葉量は地上からローテクで推定しろ!」へのリンク
== 森林の葉量の垂直分布を推定:なぜ? ==
== 携帯型レーザー距離計を使う方法 ==
森林全体の葉量を非破壊的に推定する方法は「その1 樹木の葉量は地上からローテクで推定しろ!」で紹介しました.森林の葉量が推定できると,たとえば葉量が違う複数の森林間では光合成生産力がどれくらい違うかといった問題に対し,説明や予測ができます.しかし,森林の葉量がわかっただけでは,ひとつの森林の内部で起こっているさまざまな現象を説明したり予測したりすることには限界があります.かくして研究者たちは,森林の中にどれだけの葉がどのように配置されているか,にも興味を持っています.
空間のなかに葉がどれだけあるのか,は単位体積の空間あたりの葉の面積(例,m2/m3(葉面積/空間の体積=葉面積密度))や葉の重さ(例,g/m3 (葉重/空間の体積=葉重密度))などで表します.このような量を葉量密度(ようりょうみつど)と呼びます.また,葉量密度が森林内で鉛直方向に変化することを,葉量密度の垂直変化といいます.以下で「葉量密度の垂直変化」とはすべて「葉面積密度の垂直変化」のことを指すことにします.
葉量密度の垂直変化のパターンは,群落内部の光環境や,森林~大気間の二酸化炭素・酸素・水蒸気・熱の入れ替わりなどに大きく影響するので,これらに関連する研究には非常に重要な情報となります.また林冠は鳥・小動物や虫などの生息場所であることから,葉量の垂直変化はそれらの生き物の生態を知る情報としても重要です.
ここでは,森林の木を切り倒したりせず,なおかつ比較的ローコストでできる,広葉樹林の葉量密度の垂直変化を調べる方法を紹介します.
ただし,以下に述べる方法は, 「その1 樹木の葉量は地上からローテクで推定しろ!」で紹介したような方法により,森林全体の葉量が別の方法で推定できることを前提としています.ここで紹介する方法だけでは,実際の葉面積密度は現実的に推定できません.森林全体の葉量がわからない場合,以下の方法は,相対的な葉量密度垂直分布を推定する方法にしか使えません.
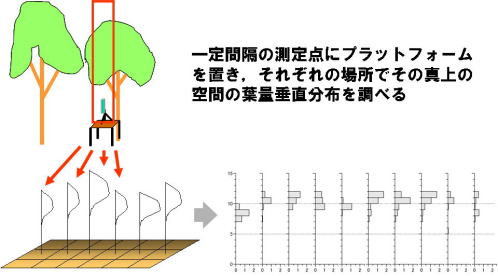
ここで紹介するのは,マッカーサーとホーンが提案した方法(MacArthur & Horn, 1969;ここではMH法と略します)に携帯型のレーザー距離計を用いた方法です.MH法では,地上から個々の葉までの鉛直距離を任意のたくさんの葉に対して測定していきます(左図).このような,葉までの鉛直距離(葉の地上高)の測定データに対し,葉が空間にどのように散らばっているかということに対する仮定をおいた計算式を適用することで,下から上を見上げたときに手前の葉に隠れて見えない葉があっても葉量密度の垂直分布パターンを推定することができます.
推定の原理や計算式は別項目(補足1:MH法はBeerLambert則と同じ」参照)で説明することにして,以下ではまず,実際にどのような測定を行うかを紹介します.
測定準備:測定に使った小道具たち
1.携帯型レーザ距離計
左の写真は携帯型レーザー距離計と呼ばれる距離測定計です.この器械についているスイッチを押すと,赤色の可視レーザーが発射されたままの状態になります(左図のように:実際には光束は目に見えません).もう一度ボタンを押すと,この器械からレーザー光が当たっているところまでの距離がmm単位の精度で測定され,モニターの表示画面に測定結果が表されます.
レーザー距離計はちょっとしたホームセンターなどで数万円で買えますが,この研究の測定に必要な機能がついている機種を選ぶ必要があります.
この測定器の写真はLeica Geosystems社の DISTO pro4aという機種ですが,すでに販売中止になっています.これと同等以上の機種で2010年現在販売されているのは同社のDISTO D8という機種(価格12万円前後)です(*).これに,器械を遠隔操作(器械にふれずにスイッチをいれて測定)できるPDAなど(5万円くらい?,合計18万円程度),が必要です.DISTO pro4aでは,PDAのかわりに,特注のリモートスイッチを使って器械本体に手をふれずに距離測定ができるようにしました.レーザー距離計には,一般のカメラ用の三脚が取り付けてあり,レーザーが真上に照射されるように設定してあります。(*2021年現在1万円以下で手に入ります!)
1-1 レーザー距離計に必要な機能
測定に必要なレーザー距離計の機能は次のとおりです.
a. レーザードット(レーザー光が当たっているところにみえるスポットライト状のレーザー光)の色が目に見えること.
b.測定対象(葉)にレーザーの反射版などを置かなくても距離が測定できること.
c. レーザー距離計に望遠鏡が附属していてレーザーがどこに当たっているか確認できる,あるいは
内蔵のデジタル画像モニターでレーザ光が当たっていところを確認できる,など,遠くにあるレーザー
ドットが何に当たっているか(何までの距離を測定しているか)を目で確認できる機能があること.
d.レーザー光のドットの大きさが,繁った葉と葉との隙間をレーザが通過できるほどに十分小さいこと;
(上の機種の場合,レーザーと測定対象との距離が10mの場合レーザーの径は6mm, 50mの場合は
3cm,100mでは6cmである;メーカー仕様書より).
これらのうち a, b, cは,レーザー光が葉以外のもの(幹や枝)までの距離を測っていないことを確認するために必要です.葉量の垂直分布を調べているのですから,葉以外のものまでの距離を測定してしまっては意味がありません.また,たくさんの葉までの距離を測定する際,レーザー光が何にも当たらずに空に抜けてしまう場合(sky hitと呼んでいます)があり,この場合レーザー距離計にはエラーメッセージが表示されます.実は,測定値の中にsky hitがいくつかあるか,も重要(後述)なのですが,エラーメッセージはいろいろな理由(たとえば測定対象物が測定中に動いた,など)で起こりうるため,レーザー光が何にも当たっていないことを確かめる上でもレーザー光が可視光であることが必要なのです.
d が満足されていない場合,例えば,レーザードットの径が30cm程度あると,レーザー光が複数の葉や枝に同時に当たってしまうため,何までの距離を測定しているかがわからなくなりますし,sky hitも起こりにくくなると考えられます.したがって,レーザードットの径が小さい事も必要な条件になります.
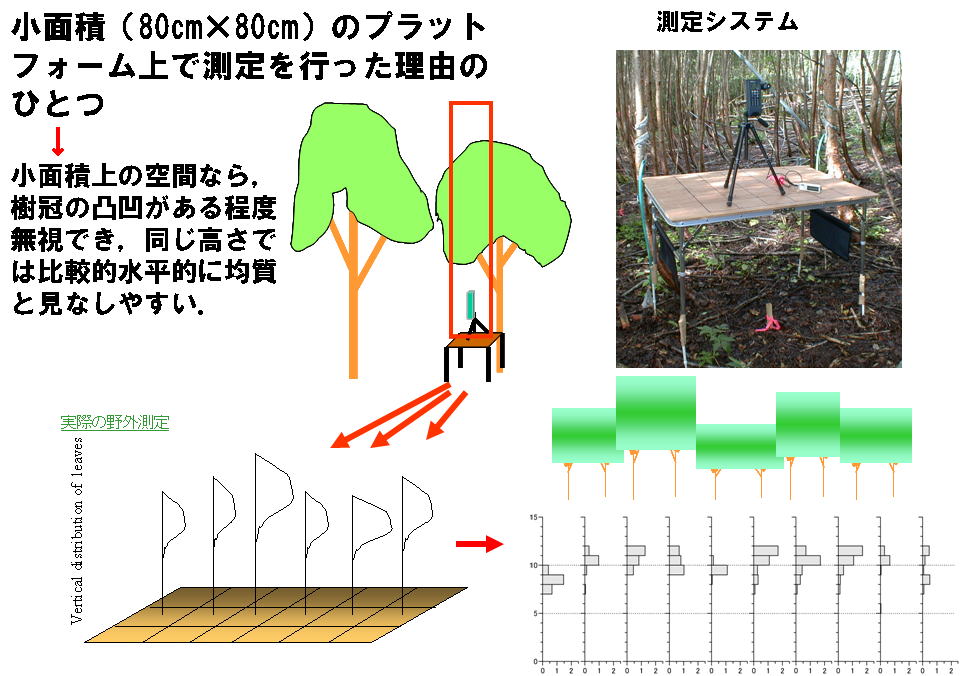
1-2. 測定システムの概要:“プラットフォーム”
レーザー距離計と三脚以外はすべてホームセンターでそろえました.下の写真が測定システムです.
折りたたみ式のキャンピングテーブルの上に,80cm×80cmの枠をマジックで画いたベニヤ板を置きました.80cm四方にした理由は,市販のベニヤ板ではそのサイズしかとれなかったからです.キャンピングテーブルの4本の足には,プラスチック製の細い「つっぱり棒」(ある程度長さが調節できる棒)を1本ずつガムテープで固定しました.水準器(気泡で地面が水平かどうか調べる器具)をベニヤ板の上に置き,ベニヤ板が水平になるように4本の「つっぱり棒」の長さを調整しました.レーザー距離計は,レーザーが鉛直・真上に照射されるように三脚で調整してあります.したがって,この板の上では三脚ごとレーザー距離計を動かすかぎり,レーザ光は常に鉛直方向に照射されますし,レーザー距離計の地上高も一定に保たれます.
これで測定システムは完成です.この測定システムを作る前に,レーザー距離計をカメラ用の一脚あるいは三脚にとりつけただけの状態で,テーブルを使わない方法を試してみました.しかし,たくさんの葉を測るたびにレーザーを鉛直に向けるため一脚あるいは三脚を調節するのに時間がかかりました.さらに,一脚の場合は,レーザーが葉に当たっているかどうかを確かめながらレーザーを鉛直に照射することができませんでした.結局,上のような「プラットフォーム」を組んでから測定するのが一番早いことがわかりました.
野外(森林内)での測定方法
調査をする森林内のなかで,まず上のプラットフォームを置く場所を10カ所選びました.調査プロット(ダケカンバ林)が20m×30mだったので,調査プロットを横切る直線上に約3m間隔で10カ所に杭をうっておき,そのそれぞれにプラットフォームをおいて測定することにしました(下図).
各々の測定点では次のようにして測定を行います.レーザー光を真上に照射しっぱなしの状態で,レーザーが枝や幹に当たっていない事を目で確認し,距離測定を行います.レーザーが葉にあたっていれば葉までの距離を記録し,sky hitになったときはそうであることを記録します.一度測定がおわったら,距離計を三脚ごと10cm程度任意にずらし,再度同じように測定を行います.これを,プラットフォームの上で25~36回繰り返しました.つまり,25~36個の測定値(葉の地上高またはsky hitの記述)がひとつのプラットフォームで得られることになります.1カ所の測定点での測定時間は20分程度でした.風が強いと枝ごと葉が揺れて測定できないことがありました.
1カ所の測定点のプラットフォーム上で行う距離測定の繰り返しの回数は,その森林の葉量(註1)がどれくらいあるかによって異なります.測定する森林の葉量に関する情報がまったく無い場合,葉が平均的に45度傾いていると仮定すると,落葉広葉樹林なら最低100回ほどあったほうが望ましく,常緑広葉樹林では500回以上必要な場合があります.森林の葉面積指数を推定する方法のひとつは「その1」で紹介しました.
(註1;ここで言う葉量とは葉面積指数(LAI ; leaf area index)のこと.単位土地面積上の葉の面積の総和をm2/m2(葉面積/土地面積)で表したもので,日本の場合,落葉広葉樹林なら3~6m2/m2,常緑広葉樹林なら6~9 m2/m2程度であることが知られています.)
レーザーで測定した葉のデータを葉量密度に変換する方法
計算原理は別に示すことにして,ここで測定データをどうやって葉量密度に変換するかを説明します.計算方法は実に簡単です.
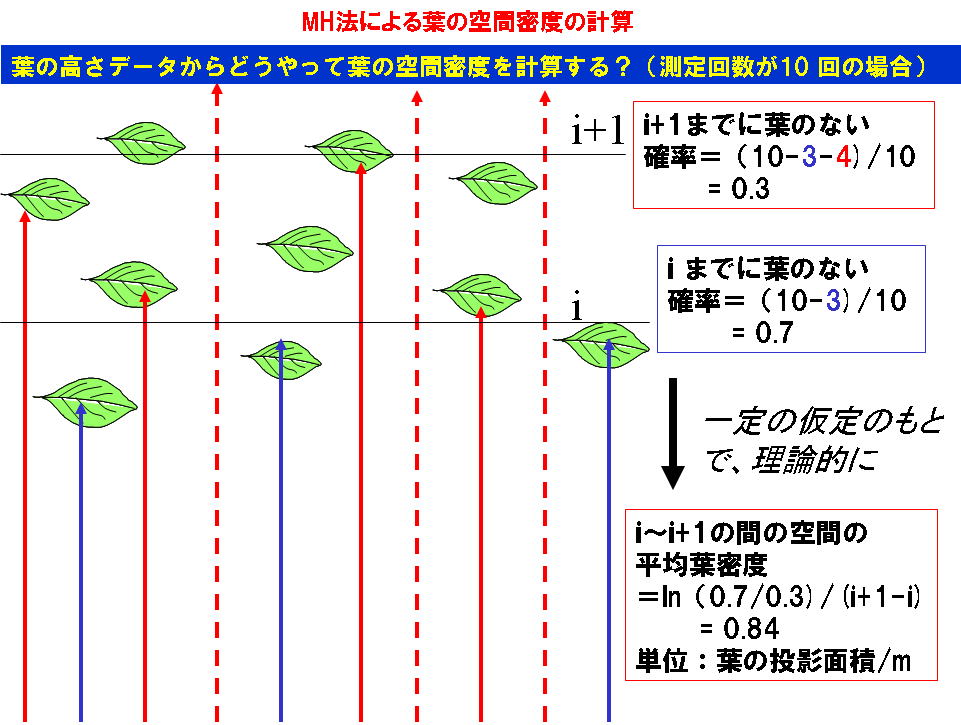
林床のひとつの場所においたプラットフォーム上で,地面から上向きにレーザーをN回発射し,ある高さ hi (m)までに葉に遮られずに届いたレーザ光線の数を ni, さらに, hi+1 (m)の高さも通り抜けたレーザー光線の数をni+1 とします.このとき,この二つの高さに挟まれた層の葉量密度はLDMHは
LDMH=ln{(N-ni)/(N-(ni + ni+1))}
です.ここで,「ln」は自然対数を表す記号です(つまりloge と同じ).また,葉量密度の単位は,単位空間の体積当たりの葉の投影面積
[m2/m-3]
または 深さ1mの層あたりの葉の存在確率
[m-1]
で表します.このような計算を,地上から1mの層ごとに計算してやれば,葉量密度の垂直分布が計算できます(まだ完成ではありません).後者の単位は,もともとこの方法が「ある層のなかに葉が存在する確率」を推定する方法として考え出されたためこのような単位を用いていたのです(左図).
(詳しいことを知りたい方は,補足1をご覧ください.)
このように,1つのプラットフォーム上で,
1)レーザー距離計を置く位置を少しずつずらしながらN回上向きにレーザーを発射し,そのたびに葉の高さを記録する.
2)レーザーが葉に当たらず空に抜けた場合(sky hit)もN回に含まなければならない.
3)そのようなN回の葉の高さの測定値を地上高1mごとの層別に分け,数を数える.
という方法でエクセルなどのデータシートに整理しておけば,プラットフォーム上の葉量密度垂直分布の計算が簡単になります.
MH法の林分平均の葉量密度の垂直分布の計算
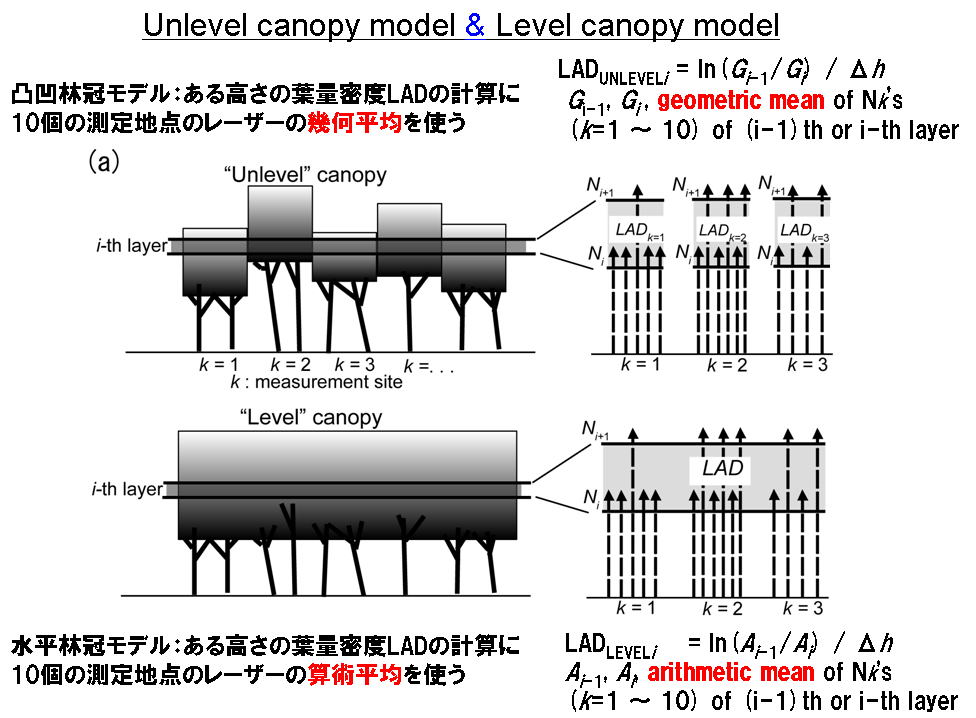
つぎに,各測定地点で測定したデータから林分の平均の容量密度の垂直分布を計算する方法を説明します(ここではまだ葉の傾斜角は考慮に入れていません).これには大きくわけて次の2つの方法が可能です.ひとつは,凸凹林冠モデル(unlevel canopy model),もうひとつは水平林冠モデル(level canopy model)です.どちらもMH法の計算方法にしたがって葉量密度の林分平均値を計算するのですが,データのまとめ方が違います.
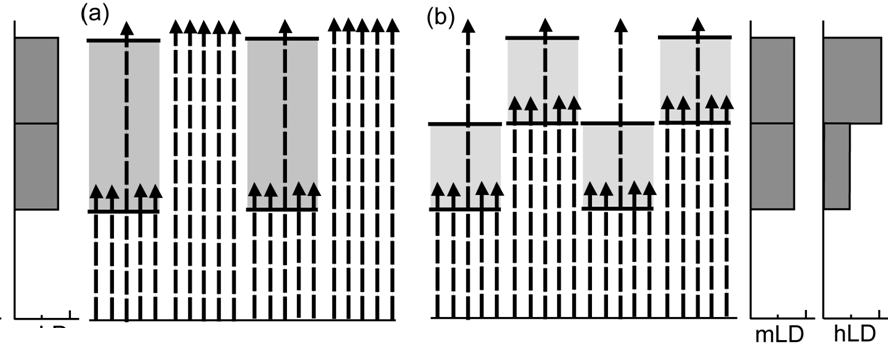
凸凹林冠モデルでは,測定地点ごとに各地上高の葉量密度を計算し,葉量密度の測定地点間の平均値を計算します.しかし,別の計算方法も可能です.それは,ある地上高の水平な層に入ってきたレーザ数の測定地点間の平均値とその層を出て行ったレーザー数の平均値からその層の葉量密度の平均値を計算する方法です.これは,林冠が水平で,林冠内では水平方向には均質であると仮定しているのと同じことになります(上の図の下側).後者の方法では正しく森林全体の平均的な葉量垂直分布が計算できないため,後者の計算方法をとるべきではありません.後者の方法をとると,例えば下の(b)のように,林冠が凸凹している場合,実際の葉量垂直分布は「mLD」と書いてあるところの上の葉量垂直分布であるはずなのに,計算上「hLD」と書いてあるところの上のような,実際とは違う葉量垂直分布に計算されてしまいます.また,下の(a)のように,ある場所では林冠が存在し,別の場所では林冠が存在しない不均質な森林の場合も,森林全体の葉量が実際よりも過小評価されてしまいます(理由の詳細は省略).
プラットフォームを使用した測定は,そのほうが早く測定ができるから,と説明しましたが,もうひとつ重要な意味があります.1つの測定点の面積が大きければ大きいほど,同じ高さに上の図の(b)のような「葉がある空間」と「葉がない空間」が混じった不均質な空間を測定してしまうことになります.小面積のプラットフォーム上で測定を行うことは,それを少しでも軽減させるという意味もあります(下の図).
ただし,ここで注意すべきことがあります.それは,MH法で計算される葉面積密度は,実際の葉面積の空間密度ではなく,水平面への葉の投影面積の空間密度だということです.
もうひとつあったほうがよい測定;葉の傾斜角の垂直分布
レーザー距離計でマジメに葉量垂直分布を調べる場合,本当は葉の傾斜角の垂直分布(個々の葉がどれくらい傾斜していて,それが地上高によってどう変化するか)も調べる必要があります.ここではその方法もいちおう紹介しますが,興味がなければ読み飛ばしてもかまいません.また,調べたい森林の葉面積指数がわかっていれば,葉の角度を考慮した場合としない場合とで推定される葉量垂直分布のパターンはそれほど大きく違いません.このへんの詳しいことはSumida et al (2009)にかいてありますので,より専門的に調べたい方は参考にしてください..
なぜ葉の傾斜角が必要か
自然状態の樹冠,とくに,樹冠の上側の葉は樹冠下側の葉よりも大きく傾いているのがふつうです
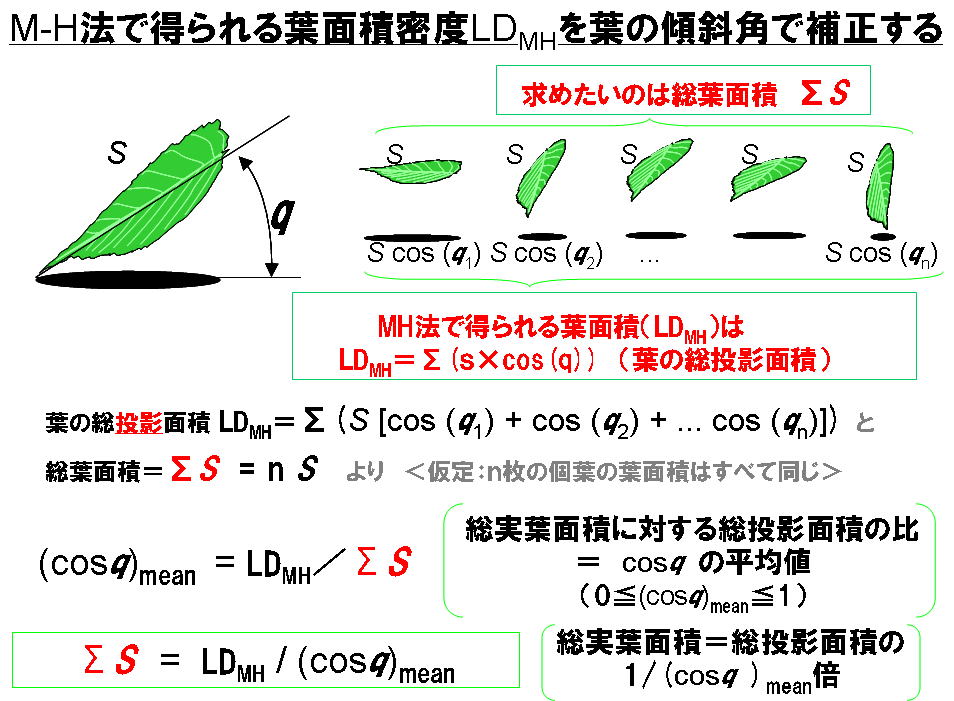
.葉の傾斜角が樹冠の上側と下側とで異なっていると,レーザー距離計で調べる葉量垂直分布のパターンにひずみが生じます.その理由は,葉が傾いているほど葉がレーザ光にあたる確率が低くなるからです.下の図の左は面積がsの1枚の葉が角度qだけ傾いています.このとき,レーザー距離計とMH法の計算式で推定される葉の面積は,水平面への葉の投影面積(黒い影の部分の面積),すなわち,sではなく s×cos(q)になってしまうのです.同様に,その層全体の葉面積密度推定値も Σ(s×cos(q))になってしまいます.
そこで,1mおきの地上高の層(たとえば地上高9~10m)でたくさんの葉の傾斜角を調べて,補正してやりましょう.1枚1枚の葉の面積は皆同じ(s)と仮定し,この層で n枚の葉の傾斜角q1,q2,・・・qnを測定したとしましょう.また,それぞれの傾斜角のコサインの値の平均値を(cos q)mean(= [Σcos(q)] /n )とおきます.このとき,MH法で得られたこの層の葉面積密度がLDMHなら,この層の実際の葉面積密度 SACTUALは
SACTUAL=LDMH/cos(q)mean (実際の葉面積密度=MH法で推定した葉面積密度/葉の傾斜角のコサインの平均値)
で求められます.角度qの平均値(平均角度qMEAN)のコサイン(cos(qMEAN))で割ってはいけません(詳しくはSumida et al (2009)参照).
葉の傾斜角の測定機器
葉の傾斜角の測定には,デジタル傾斜計(下の写真,右)をつかってしらべました.
デジタル傾斜計はMacklanburg-Duncan社のPro3600という機種名ですが,日本で取り扱っている業者もたくさんあるようです.測定はかんたん,傾斜角を測定したいものに傾斜計の下面をあわせると(つまり傾斜計を傾けると)リアルタイムで傾斜角が表示されます.写真では12.1度傾いています.その状態のままボタンをおすと,表示されている角度計測値がロックされ,読み取ることができます.ただし,やはり特注で,リモートスイッチ(片手で葉の傾きにあわせて葉の角度をはかり,もう片手でスイッチを押す)と,測定値を自動的に蓄積するPDA(ヒューレットパッカード社,HP iPAQ hx2490b)をつけてもらいました.全部で16万円くらいでした.
なお,デジタル傾斜計の上には小さな水準器(気泡で水平かどうかがわかる)がつけてあります.傾斜計はこの写真上では左右方向だけの角度を測るので,写真上で前後方向に傾いていると正確に傾斜角が測定できないからです.
調査を行った森林では,幸いなことに,林冠にアクセスするための足場(簡易タワー)が建っています.これに登り,そこから手の届く範囲で,上の傾斜計をつかって地上高1mごとに葉の角度を調べていきました.1mの層について,少なくとも100枚以上の葉の角度を測定しました.各々の1mごとの層内では,小枝を数本ランダムに選び,その小枝の葉をすべて測定するようにしました(葉をランダムに選ぶようにすると,選ぶ葉の角度に対する主観が入りそうだったので).1日に,樹冠の上から下まで約1000枚の葉の角度を測ることができました.
== 結果(1):葉の傾斜による補正値の垂直分布 ==
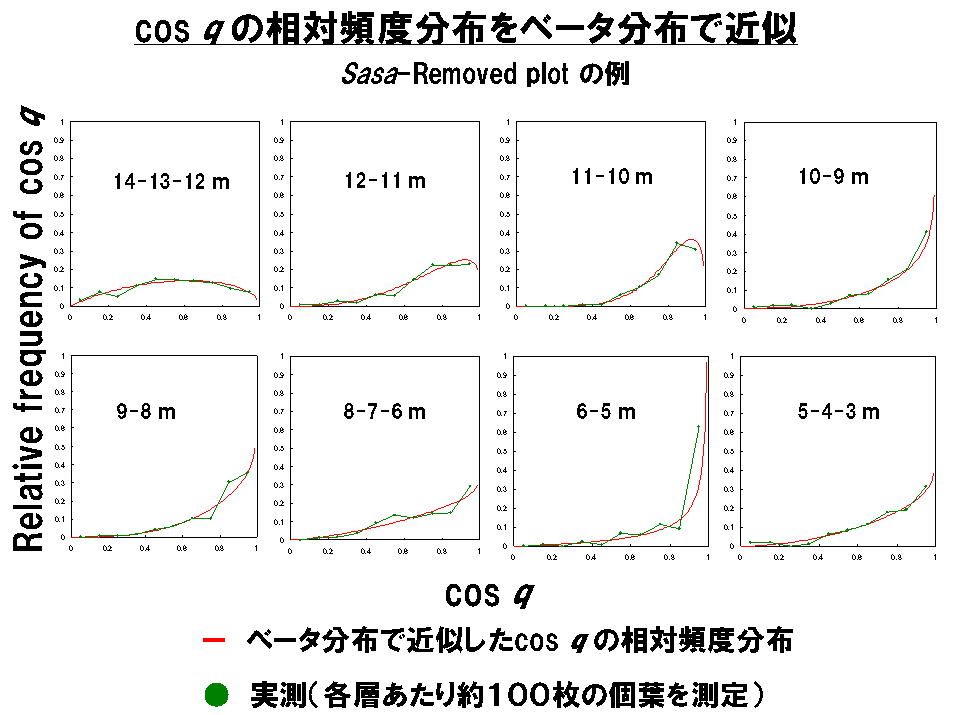
二つのダケカンバ林調査プロットに一基ずつある林冠観測タワーから測定した葉の傾斜角測定結果をもとに,角度qのコサインcos(q)の頻度分布を地上高(図中に示した)ごとに示しました.下はそのうちの1つのプロットの例です.横軸はcos(q)の値で,0から1まで値がとってあります.つまり,各グラフの横軸が左(0)に近いほど葉が傾いており,右(1)にいくほど葉が水平であるということになります.
この図は,Sumida et al(2009)の校閲者が「こんな図は興味ない」と言って削除させられたものですが,参考のためにお見せします.
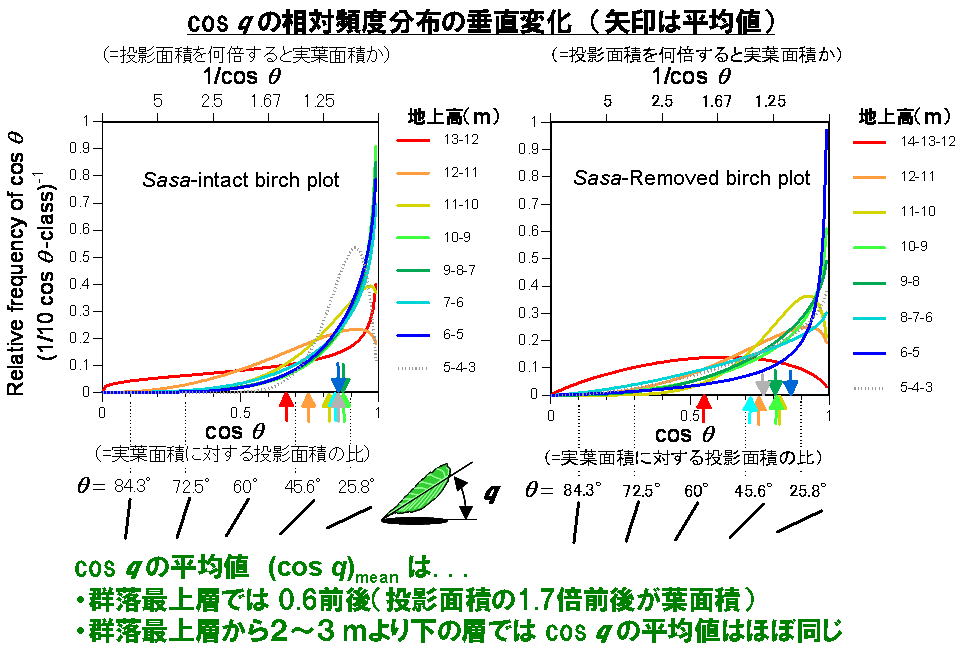
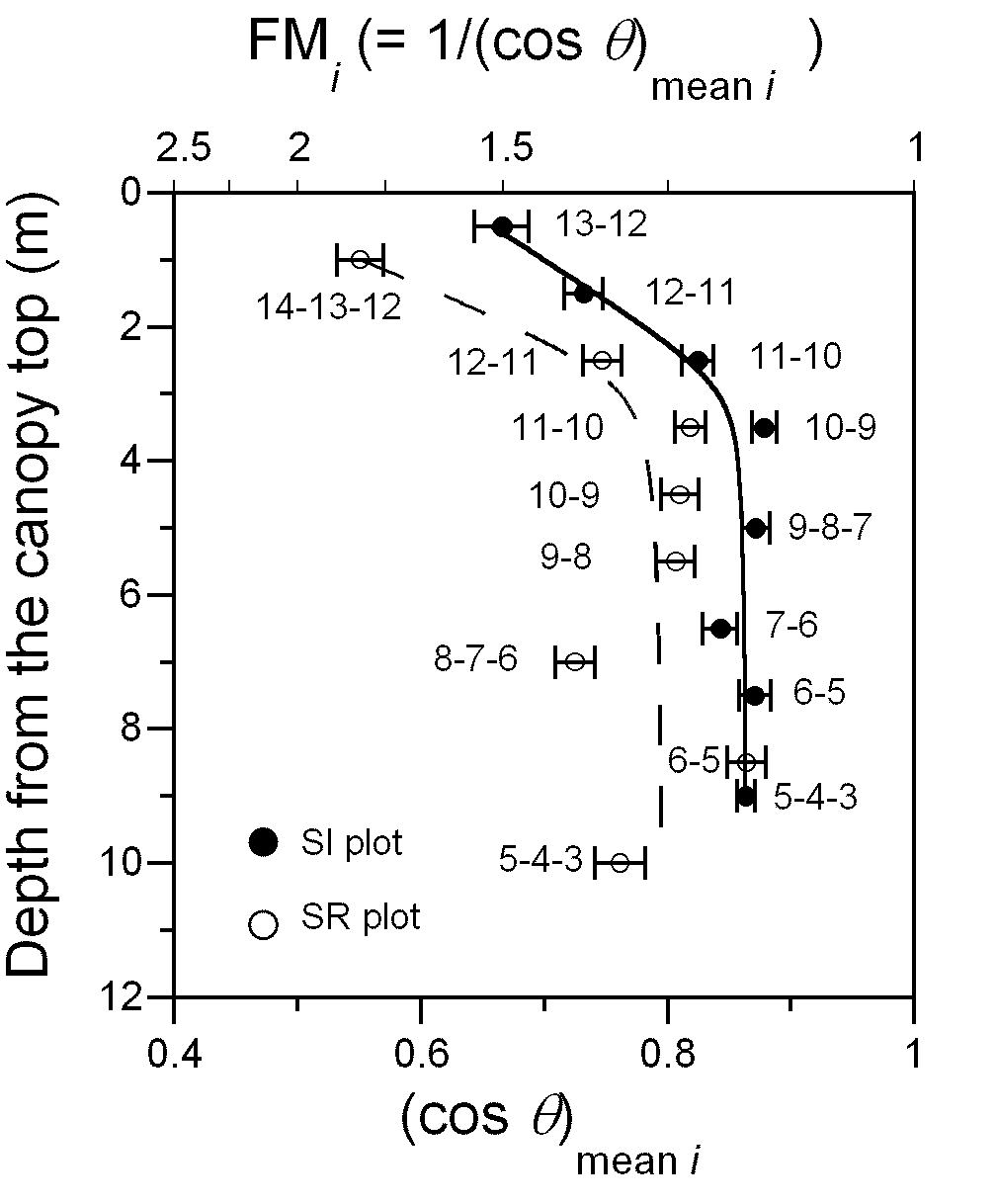
実測データ(緑の折れ線)をベータ分布という頻度分布に当てはめると非常によく合うことがわかったのですが,当てはめた理由にはここでは意味がありません.(本当はベータ分布のパラメターが上の層から下の層にいくにしたがって変化する様子をモデリングしようと思ったがややこしいのでやめた.) この図を1つにまとめると,下の右のようになります(左はもうひとつのプロット).矢印は葉の傾斜角のコサインの平均値 (cos q)mean を表しています(一部qのかわりにθになっててすみません).だんだん平均値が右にずれていく様子がわかります.横軸の下に,コサインに対応する葉の角度が書いてあります.林冠最上層では45度ぐらい葉が傾斜しているので,コサインの値は0.6ぐらいです.これは,MH法で推定される葉の投影面積が実葉面積の0.6倍程度しかないことを表しています.したがって,MH法で推定される葉面積の空間密度を 1.7倍(1/0.6)しないと実際の葉面積の空間密度にならないことになります.
この,MH法で推定した葉の投影面積の空間密度を実際の葉面積の空間密度にするために何倍しなければならないか,は
1/(cosq)meanで与えられます.この値をFM(factor of multiplication)と呼びましょう.林冠の最上層から下にいくにつれてFMは減ってきますが,林冠の最下層でもFMは1.3ぐらいで落ち着きます(下図).下の図中の数字は地上高です.
上の図は Sumida et al (2009)のFig.4を詳しくしたものです.林冠最上層から3~4mより下では葉の傾斜角がほぼ一定になることがわかります.
== 結果(2)MH法による葉量密度垂直分布 ==
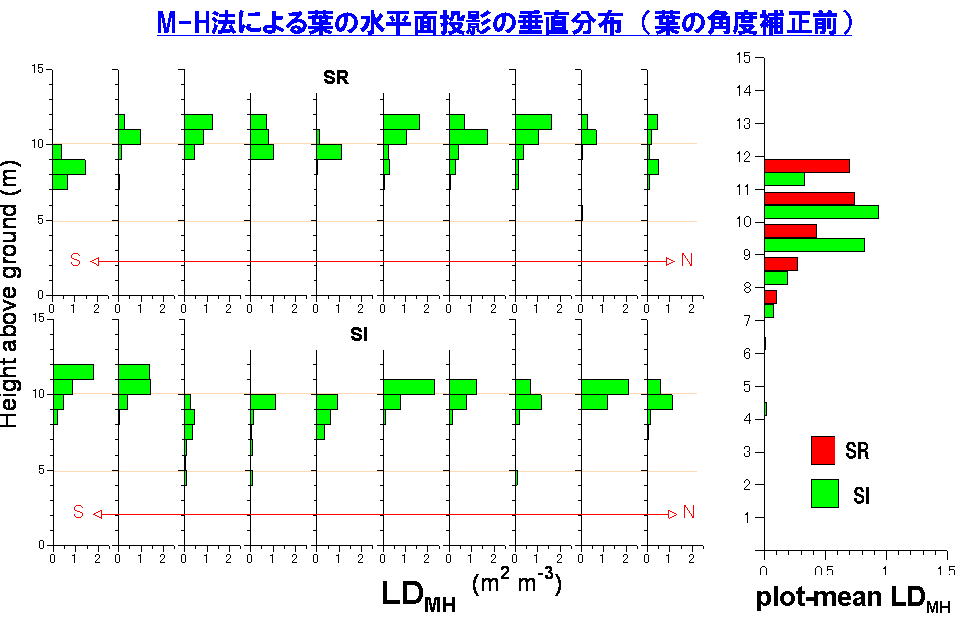
まず,林床上の10地点においたプラットフォーム上での葉量垂直分布を測定地点ごとに示します.下の図には二つのダケカンバ林プロット(SR, SI)の結果が示してあります.この図は,Sumida et al(2009)には載せていない図ですが,説明のためにお見せします.
上の図の右側には,MH法で推定した各測定地点の各地上高の葉量密度LDMHのプロット当たりの平均値を高さごとに示したものが描いてあります.すなわち,各地上高のLDMHの平均値です.しかし,これには葉の傾斜角の影響は何も考慮されていません.さらに,アロメトリー法による両プロットの葉面積指数(註1および「その1 樹木の葉量は地上からローテクで推定しろ!」参照)は,SIプロットで4.56 m2/m2, SRプロットで4.57 m2/m2でしたが,各プロットごとにすべての地上高ののLDMHを全部足してもこの値になりません.その大きな理由のひとつは葉の傾斜角の補正がされていないこと,もうひとつの大きな理由はレーザーの発射数が少ないからなのですが,レーザーの発射数が少なくても,MH法で調べた葉量密度の垂直変化パターンは相対的な分布形としては信頼できることがわかっています.
各プロット内の10地点でとった上の結果から,葉の傾斜角の影響も考えながらプロットの平均的な葉量垂直分布に換算するときは,いくつかの方法が考えられます.
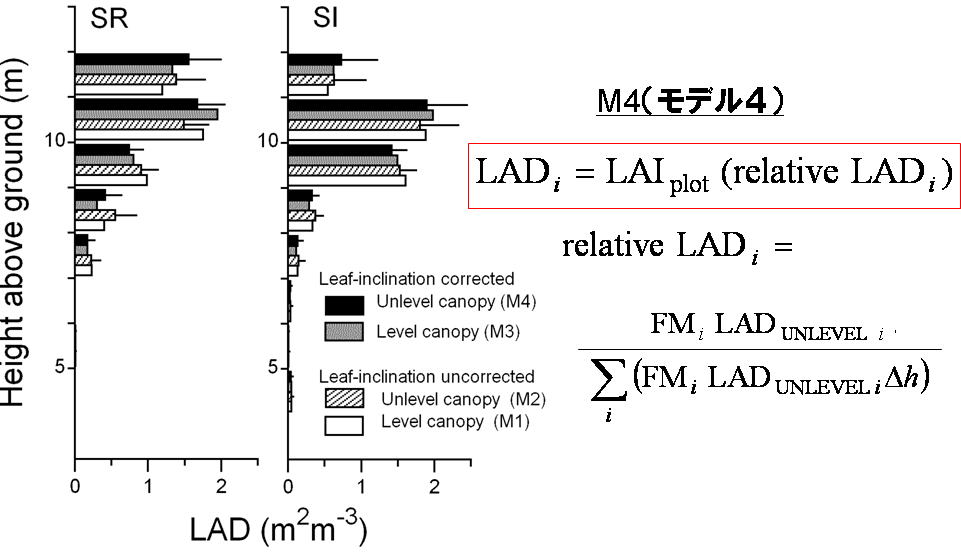
ここでは,もっとも詳細な方法(したがって最も正確なはずの方法)の説明をします.上の図で,M4(モデル4)と書いてあるものがその方法です.その計算式は図中に書いてあります.ここで,LADiは i番目の地上高の層の葉面積密度,FMi はその層の葉の傾斜角補正係数(=1/(cos q)mean), また,LADUNLEVELi, は,凸凹林冠モデルで計算した,i 番目の層のMH法による葉面積密度の測定地点間のプロット平均値(ひとつ前の図のplot-mean LDMHと同じ),LAIplotは,アロメトリー法で推定したプロットの葉面積指数(註1参照)で,SIプロットは4.56 m2/m2, SRプロットは4.57 m2/m2です.葉の傾斜角はそれぞれの調査地点に一基ずつしかない林冠観測タワーから測定しただけなので,葉の傾斜による補正値FMiは地上高だけで決まる(測定地点が違っていても地上高が同じなら補正値も同じ)と仮定しました.この補正値は,葉の傾斜角の図の解説で示した,各地上高のFMの値です.
上の図には,比較として葉の傾斜角の補正をした場合(M4,M3)としなかった場合(M2,M1),および,凸凹林冠モデルで計算した場合(M4,M2)と水平林冠モデルで計算した場合(M3,M1)が載せてあります.
葉は林冠最上層ほど大きく傾いていたため,,葉の傾斜角を考慮して補正すると,補正しない場合より葉量密度が林冠上層に集中する傾向が強くなります.SRプロットでは林冠上層に葉が偏る傾向があったため,特にその傾向が強くなりました.また水平林冠モデルより凸凹林冠モデルのほうが,やはり葉量密度が林冠上層に集中する傾向が強くなりました.
一方,葉の傾斜角による補正係数(FMi)は林冠最上層では1.5以上でした.このことは,MH法による葉量密度の計算結果(各地上高のLDMH)に葉の傾斜角による補正を直接施すとLDMHの1.5倍が実際の葉量ということになりますが,上の結果ではそうなっていません.M1~M4の方法のように,直接林分葉量がアロメトリー法など別の方法でわかっている場合(「その1 樹木の葉量は地上からローテクで推定しろ!」参照)には,森林全体の葉量は予め森林全体の葉量が固定されているので,葉の傾斜角の補正はFMiの値ほどには効いてきません.葉の傾斜角補正後のMH法の葉量密度を各測定地点ごとにもう一度相対値化し,その後で森林全体の葉量(LAIplot)を各地上高に配分するからです.この二つのダケカンバ林の場合,葉の傾斜角による補正よりも凸凹林冠モデルで計算することのほうが重要なように思います.
なお,某有名ログの1ページのMacArthur-Horn法解読の部分に「•さらに本日の検討によって, 低温研某研究室伝来の変体 M-H 法はアヤしいものだ, とわかった. この方法, データが「足りない」状況でごまかしを混入させると, とんでもない垂直葉群分布を生成せしめるんだよね. けっこう面倒だ. どうにかならんものかね」と指摘されています.このような指摘,実はずっと以前からなされていました.とくに,MH法の測定をそのまま葉の投影面積の空間密度として使おうとするととんでもないことがおこります.一方,上の方法のように,林分葉量をアロメトリー法などの別の方法で推定し,MH法の測定結果は相対的な葉量密度の垂直分布を推定するためだけに使う場合はそれほどとんでもないことにはならないことも知られていました.
とは言え,MH法で推定できる葉量密度の垂直分布は,厳密なものを推定しているわけではありません.補足1にも説明してありますが,MH法はBeer-Lambertの法則において吸光係数K=1とおいたものと同じです.したがって,MH法でうまく葉量密度の垂直分布が推定できるのは,Beer-Lambert則が成立する条件(1枚の葉が土地面積に対して十分小さく,その土地の上の空間では個々の葉がその上下の葉の位置に無関係にランダムな水平位置をとる)と同じです.この条件と現実の森林状態との間に差があることを考慮に入れて結果を解釈する必要があります.
back to the page top
<<< 補足1 >>>
補足1(pdfファイルへのリンク324kb):別ウィンドウで開きます)
・↑MH法は実はBeer-Lambertの法則と同じ,ということが説明してあります.
<< MH法のオリジナル論文 >>
MacArthur, R.H. and Horn, J.W. (1969) Foliage profile by vertical measurements. Ecology 50(5), 802-804. JSTORのページへリンク
back to the page top